我们都知道,π是圆的周长与直径的比值。
π=3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385…
数据科学家曾使用种种艺术方式将π值可视化,其中最广为人知的是生物信息学家Martin Krzywinski,Krzywinski使用计算机科学和统计学来理解生物数据,他从2013年开始发表他的“π的艺术”,一切都从下面这张可视化图片开始:

made by Martin Krzywinski
在这张图片中,圆周率的每一个数字都由一个不同颜色的圆点表示:比如3是橙色,1是红色,4是黄色,等等。然后,Krzywinski将这些彩色的圆点进行变换折叠,使他们呈螺旋状从圆的中心向外依次排列,下面这张图,就是圆周率的前13689位数:

made by Martin Krzywinski
Martin Krzywinski与Cristian Vasile的合作则被他们自称为“艺术家之间的碰撞”,Krzywinski创造过一系列π的圆形艺术图案,就如下图,圆周被10等分,每一段代表从0-9的一个数字,而π中每一个数字则变成圆的一根“和弦”,创作者从代表“3”的圆周开始,向代表“1”的圆周画一条线,再向4、1、5、9、2、6不断连接,并用不同的颜色进行区分。
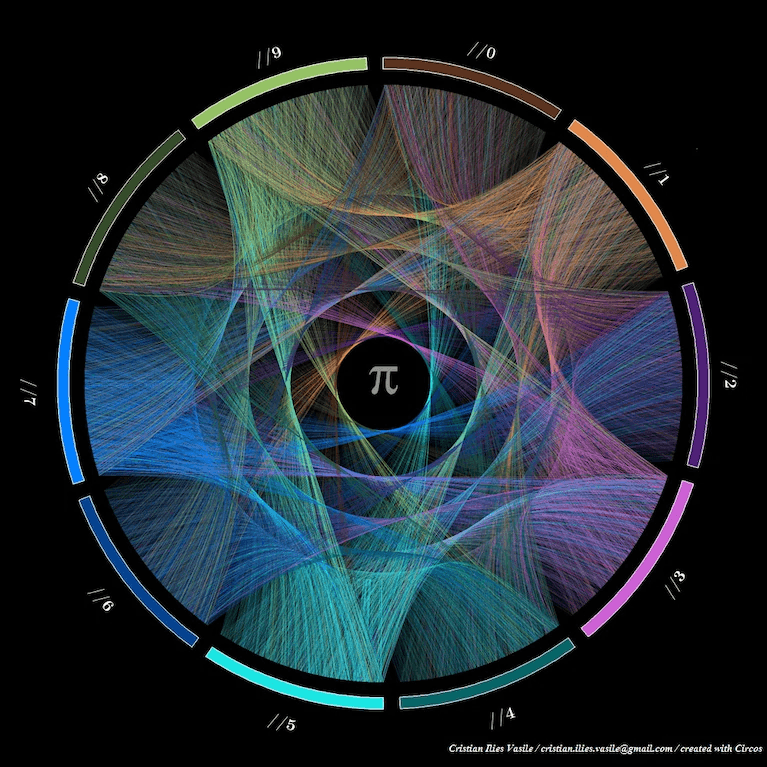
下面的图片同样遵循这个过程,但它们之间的区别是:当π中出现连续两位相同的数字(如小数点后第24和25位都是3),Krzywinski和Vasile就在边缘点上一个圆点,数字重复的越多,圆点就越大。
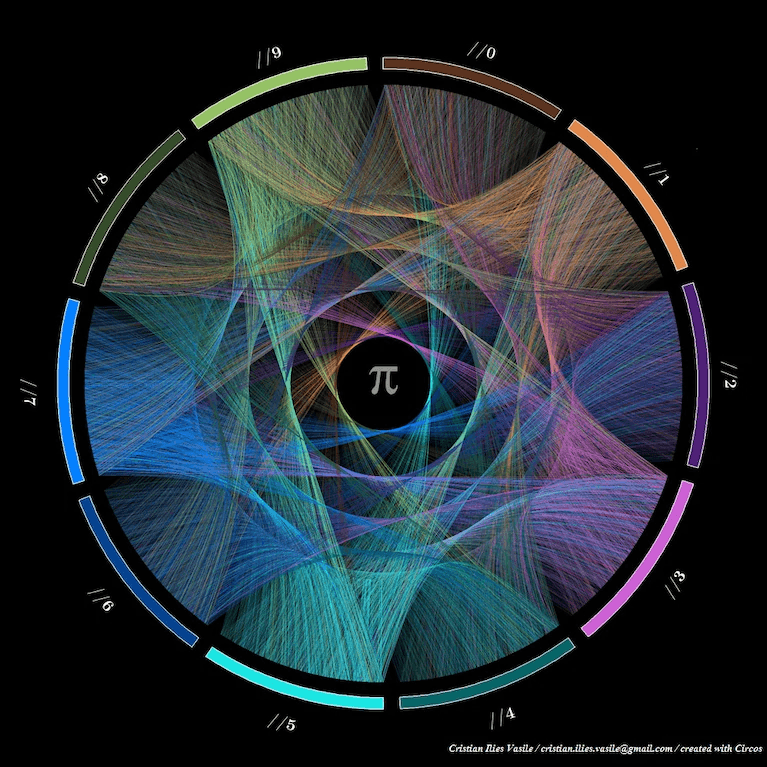
圆上方最大的紫色圆点是一个特殊点——从π的小数点后762位开始,出现了连续的6个9,物理学家费曼曾经在讲课的时候打趣说,自己只要背到那一点,就能说“999等等”,并且假装π是个无限循环的有理数,于是这个点被称为“费曼点”。但从概率上讲,这个连续重复出现的时间要比概率所预计的早得多。
下面是Krzywinski在2015年制作的新的图片,这个类型被称为“树状图”,他先画出垂直的3条线将方框分开(代表π的第一个数字3),然后在第一个框中水平地画出“1行”、在第二个框中画出“4行”,以此类推。krzywinski还在里面以随机颜色填充图形,这种颜色正是19世纪20年代包豪斯艺术运动主要成员青睐的三原色。

那么……这一切有什么意义呢?即使大部分作品都足够美丽有趣,也仅仅是让人欣赏而已。但krzywinsk有自己的看法,他认为艺术能够唤醒人们对数学的情感——尤其是厌恶和困惑以外的情感,比如希望——并由此开始和数学与随机性的对话。
“所有的数字都有自己独特的趣味。”Krzywinski说,“但与奥威尔的《动物庄园》的结局相呼应的是,有些数字比其他的更有趣,π就是其中之一。”
为什么这么评价圆周率?一方面,π描述的是一个完美的圆,因此无论当π在任何公式中出现时,它都代表了一个圆圈或者某种重复的轨迹,从心脏跳动到地球围绕太阳公转的轨道都是如此。
另一方面,π的数值概率是“随机的”(或者更准确的说,是“均匀分布的”)——这意味着,当π的数值被无限推导下去时,出现0到9的概率是相等的。事实证明,在圆周率的前60亿位数字中,从0到9每个数字都出现了大约6亿次。
“如果π真的是随机的,那就意味着π中的数字序列永不重复,而且会包含所有可能存在的组合形式——因为它是无限的,任何你能想到的称之为“编码”的数字都将显示在π内。”Kryzwinski说。为《纽约客》写作的康奈尔大学数学家Steven Strogatz也说,π的特别之处在于:在它的范围内,“无限触手可及”。
数学家们已经将圆周率计算到了小数点后十万亿位,没有发现明显的模式规则,看起来确实是随机的——但真正困扰数学家的是,没有人可以肯定地说,π就是随机的,目前没人提出数学上的证明。因此,从另一个意义上说,圆周率又不能称为“随机数”,毕竟,数字本身体现的是一种完美循环的顺序。“在有序和无序之间的张力,是π最诱人的特征之一。”Strogatz写道。
π的随机性可以由另一个可视化的图片说明,它的作者是Nadieh Bremer,一位爱好数据分析和视觉艺术的天文学家,Bremer说,她从Krzywinski的工作中获得了灵感,可以用π的数字制作衣服地图,每个数字的都代表着一种颜色和方向。
Bremer特别指出,这种想法已经提出了很长时间,在1888年的书籍《机会的逻辑》中,数学家John Venn曾提议用0-7代表八个方位,用π的数据来制作跟踪路径,Cristian Vasile也曾使用π随机游走,在地球表面映射图像。
Bremer的可视化图形是使π遍历了小数点后100位,1000位,1万位,10万位和100万位数字得出的,图像如下:
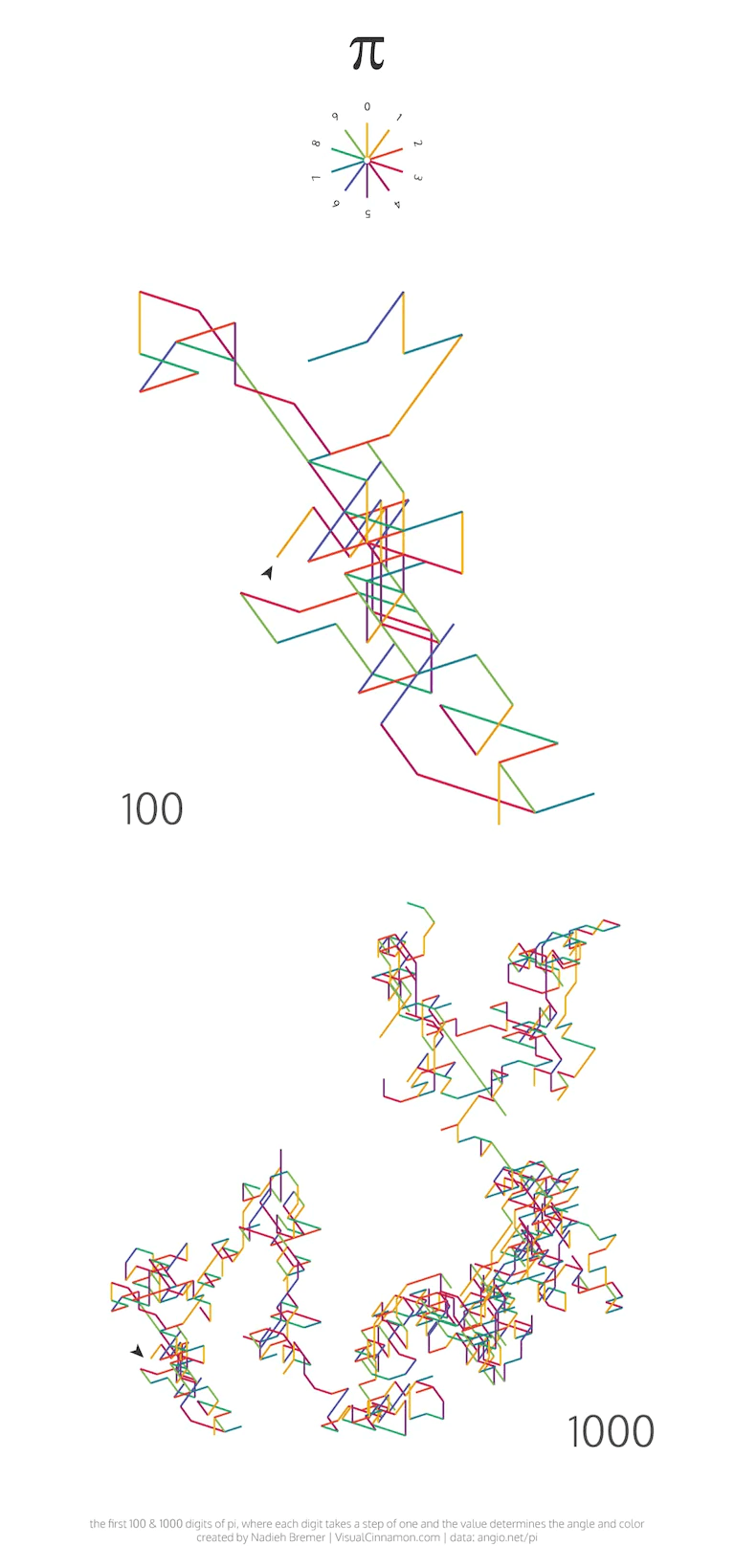
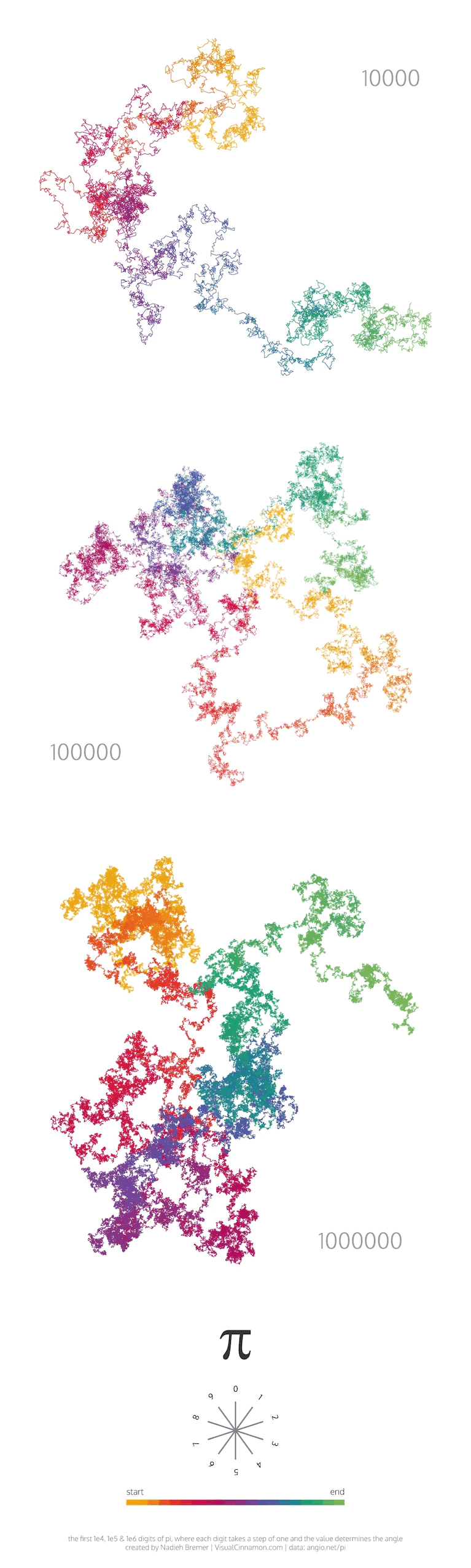
Bremer说她最喜欢的部分是,可视化图片中小数点后1000位与1万位的数字形状没有明显关系,即使看到了1万位数的图片,你也不知道10万位数的图片会长成什么样子。Bremer将其描述为随机性的缩影:过去不会影响未来,π不存在明显的结构或者规律。
我们还能从这些图形里收获什么?首先,在二维空间内看到的圆周率的所有数字,都能够带给人一种关于数学的态度:数学不仅仅是页面上的数字,从物理学到建筑师,数学是我们用来描述和构建世界的语言,π尤其如此,它描述了自然界中处处可见的一个完美的圆。
Kryzwinski说,“π日是一个伟大的时间,在这一天,你可以花一点时间和精力来了解这一切,了解数学如何作为一种语言来描述现实,书写我们在宇宙中的工作细节。”
“多亏了数学和数字,我们才能构建出将这篇文章传递给你的设备,当你读到它的时候,我们会知道光子有多快,当他们击中你的视网膜时会发生什么,剩下的就看你的了。”
👍
这篇有趣的文章 10 stunning images show the beauty hidden in pi 由 Ana Swanson 于2015年3月14日 发表在 washingtonpost.com。


