这里定期分享科技、信息技术、商业、医学及人文资讯,每周日发布。欢迎投稿或推荐线索。
封面主题:飞机坟场

飞机坟场指的是美国亚利桑那州图森市附近的戴维斯-蒙森空军基地(Davis–Monthan Air Force Base)“航空航天维护与再生中心”,美军退役飞机大都会被运往该中心进行处理。如果你开车沿着美国亚利桑那州图森市的科尔布南路行驶,你会发现道路两侧联排的房屋消失之后,映入眼帘的是一番极其不同寻常的景象:一排排的军用飞机默默地停放在沙漠中,接受着烈日的炙烤。这里的军机种类多种多样,从体型庞大的货运飞机到笨重的轰炸机,从大力神运输机到因为电影《壮志凌云》而声名远播的F-14雄猫战斗机。



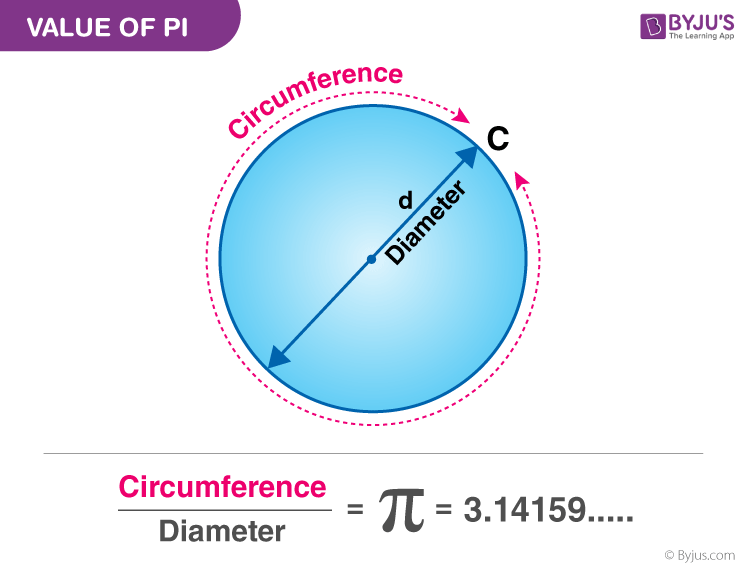

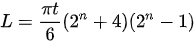 ,这里 L 代表纸张的最小长度,t 代表纸张厚度,n 代表折叠次数。
,这里 L 代表纸张的最小长度,t 代表纸张厚度,n 代表折叠次数。