山巅周刊，定期分享科技、商业、医学及人文资讯，每周日发布。欢迎投稿或推荐线索。

大家好！今天是2022农历春节公共假期的最后一天。祝您在新的一年里更多新的收获！

封面主题：软件供应链

什么是软件供应链

软件供应链（Software Supply Chain）类似于其他活动或行业。一些资源被消耗，然后通过一系列步骤和过程进行转化，最后作为产品或服务提供给客户。

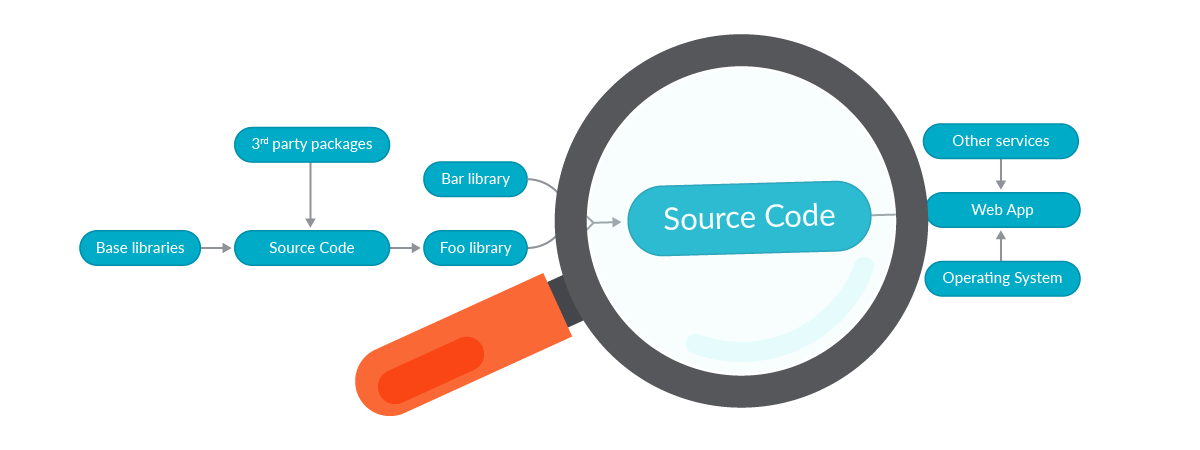
在软件中，原材料是通用库、代码、硬件和将代码转换为最终可交付成果的工具。此可交付成果可以部署为面向用户的应用程序、服务（从相同的供应链循环开始）或作为依赖项包含的另一个包工件（不同产品的一部分）。

山巅周刊，定期分享科技、商业、医学及人文资讯，每周日发布。欢迎投稿或推荐线索。

明天就是除夕，祝大家春节愉快！特别向喜欢宅以及不得不宅的读者推荐阅读清单建议和IT装备建议。

封面主题：CEO 的嘲笑

摩托罗拉、诺基亚和黑莓等手机厂商都曾推出过改变移动产业的设备。2007 年第一代 iPhone 发布，具有多点触控技术以及友好界面。2008 年，苹果应用程序商店 App Store 发布，iPhone 在品牌和生态的协同力量下，销量快速超越黑莓和诺基亚。截至2018年，iPhone 总销量超过 25 亿台，并成为盈利最多的手机制造商。

但直到惠普于 2011 年发布 HP Veer，我仍不认为 iPhone 具有独特的优势；也迷恋于自行寻找、下载和安装应用。数码极客乐于体验新技术、新产品，但也固守思维和行为惯性，喜欢以自己的经验和经历评估这些新技术、新产品，拒绝理会大众的需求（如您不曾用过的抖音TikTok，全球安装量已超过 30 亿次，全球月活跃用户达到 10 亿），此谓“因循守旧”。

《山巅周刊》定期分享作者感兴趣的科技、信息技术、商业、医学及人文资讯，每周日发布。欢迎投稿或推荐线索。

封面主题：技术天下？

2015 年 Twitter 任命联合创始人杰克·多西（Jack Dorsey）为正式 CEO，并辞去董事长职务，当时他还是移动支付公司 Square 的 CEO。2021 年 11 月，多西宣布时任首席技术官帕拉格·阿格拉瓦尔（Parag Agrawal）接替其 CEO 职务（同时，硅谷技术创业者 Bret Taylor 为新任董事长）。

印度裔美国人阿格拉瓦尔于2011年加入Twitter，担任软件工程师，并于2017年成为首席技术官。拥有斯坦福大学（Stanford University）计算机科学博士学位和印度理工学院孟买分校（Indian Institute of Technology, Bombay）学士学位。根据彭博社的统计，阿格拉瓦尔是财富 500 强公司中最年轻的 CEO，现年37岁。

迟到了卅年的个人博客之《山巅周刊》，定期分享作者感兴趣的科技、信息技术、商业、医学及人文资讯，每周日发布。欢迎投稿或推荐线索。

封面主题：特斯拉的哨子

去年12月1日，特斯拉首席执行官埃隆·马斯克又在磨斧头，在Twitter宣称特斯拉店铺上线了一只口哨 Cyber​​whistle。

这款售价 50 美元的口哨产品描述如下：“受 Cyber​​truck 的启发，限量版 Cyber​​whistle 是一款由医用级不锈钢制成并经过抛光处理的优质收藏品。口哨包括一个集成的附件功能，以增加多功能性。注意：Cyber​​whistle 是最终销售。”没有明确附件功能是什么，以及实际上还包含一个很酷的盒子。特斯拉在 2019 年推出了 Cyber​​truck，这是一款棱角分明的电动皮卡车，引起了市场极大的兴奋。

山巅周刊，定期分享科技、信息技术、商业、医学及人文资讯，每周日发布。欢迎投稿或推荐线索。

封面主题：Münchhausen

大多数人对 Münchhausen 这个词非常陌生，但它可能指一个真实的男爵、一个虚构的男爵、少年文学经典《敏豪森奇游记》、孟乔森综合症（Münchausen syndrome）、代理型孟乔森综合症（Münchausen syndrome by proxy）、网络型孟乔森综合症（Münchausen by Internet）、明希豪森三重困境（Münchhausen trilemma），或者孟乔森数（Münchhausen number）。

在数论中，孟乔森数指 Perfect digit-to-digit invariant（PDDI），一个给定基数的数字，等于其每一个数字自乘方之和。在遵循约定 0^0 = 1 的假设中，3435（= 3^3 + 4^4 + 3^3 + 5^5）是除了 1（= 1^1）以外唯一一个孟乔森数。