圆周率 π 是一个不等于任何两个整数之比的实数，它在整数 3 之后再 带上一个具有无限长度但又永远不循环的小数：π ≈ 3.1415926 · · · 。尽管人类对 π 的认知可以追溯到远古，最先对 π 值进行系统严格的估算者应当首推古希腊科学家 Archimedes（阿基米德，公元前 287—前 212 年），他得出不等式 3 + 10/71 < π < 3 + 1/7，平均值就是 π ≈ 3.14 · · · 。

祖冲之（429-500）

在我国，三国后期魏国人刘徽（生于公元 250 年左右）留下了宝贵数学遗产《九章算术注》和《海岛算经》，并创始和使用了“割圆术”即用圆的内接和外切正多边形来逼近圆的周长。割圆术为后来南北朝时期的数学家祖冲之（公元 429—500 年）的估算 3.1415926 < π < 3.1415927 提供了最基本的方法。此外，祖冲之还以很简单的分数形式给出了圆周率的约率 π ≈ 22/7 和密率 π ≈ 355/113。

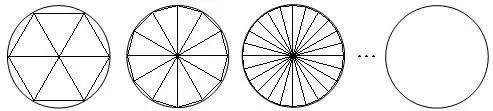
割圆术

古人计算圆周率，一般都是用正多边形来逼近圆的。Archimedes 用正 96 边形逼近圆而得到 π 小数点后 3 位的精度，刘徽用正 3072 边形逼近圆也只 能得到 π 小数点后 5 位的精度。

由于这些计算方法效率极低，估算 π 的历史进程十分缓慢。直到微积分问世以后，情况才大为改观。1706 年，英国天文学家 John Machin 发现了一个简单的解析公式并用它来计算 π 达到了小数点后 100 位的精确度：

微积分的出现，不但给出了许多关于 π 的解析估计，更大大地加快了其数值计算。且不说优雅漂亮的 Gregory-Leibniz 和差公式

以及 Wallis 乘积公式

后来发现能够用来对 π 作快速近似计算的公式还有很多。

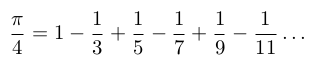
莱布尼茨方法

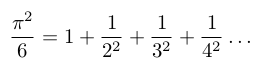
黎曼zeta函数方法